pkg.gl

解题思路

首先使用暴力递归的递归数，如下图所示：

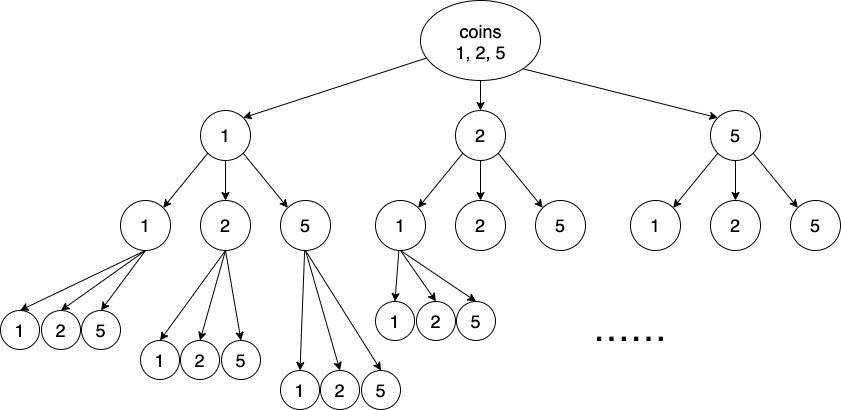
辅助函数 find，用来根据**「目标金额 amount」与「所用硬币个数 count」**来持续更新最小值，由于枝数过多必然会导致超时：

func coinChange(coins []int, amount int) int {
	res := math.MaxInt64

	var find func(amount, count int)
	find = func(amount, count int) {
		if amount < 0 {
			return
		}
		if amount == 0 {
			res = min(res, count)
		}

		for _, v := range coins {
			find(amount-v, count+1)
		}
	}

	find(amount, 0)

	if res == math.MaxInt64 {
		return -1
	}
	return res
}

func min(i, j int) int {
	if i < j {
		return i
	}
	return j
}

当我们仔细思考整个递归过程，与递归数的时候，会有如下发现：

我们不关心硬币的排列顺序，即不关心以什么顺序进行递归；
我们最终只关心这个结果的数值；
可通过 memo 来进行记忆化搜索。

重复部分如图所示：

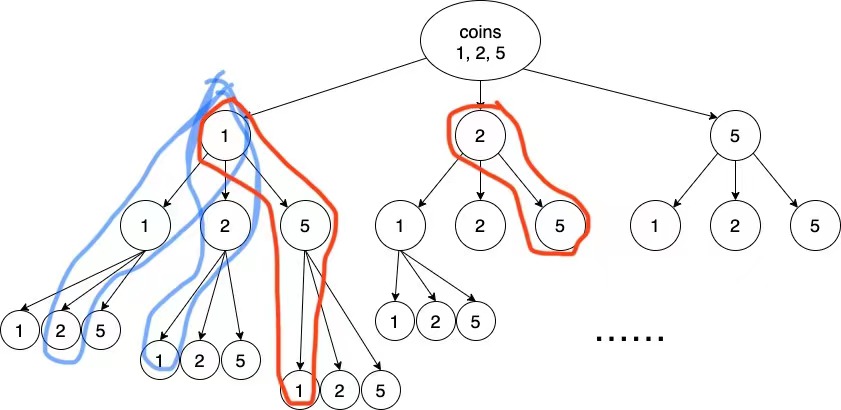
有了上面的思考，就应该清楚了 memo 代表：能组成「目标金额值」的「最小硬币个数」；现在的问题是，把 memo 放在哪？

func coinChange(coins []int, amount int) int {
	memo := make([]int, amount) // memo 代表目标和所需的最小硬币个数

	var find func(amount int) int 
    // find 用于返回能组成「目标金额值 amount」的「最小硬币个数」
	find = func(amount int) int {
		if amount < 0 {
			return -1
		}
		if amount == 0 {
			return 0
		}

		if v := memo[amount-1]; v != 0 { // 不等于 0 即为已记录过该总和，或认其无效即负一
			return v
		}

		tmpMin := math.MaxInt64
		for _, v := range coins {
			res := find(amount - v)
			if res >= 0 && res < tmpMin {
				tmpMin = res + 1
			}
		}

		if tmpMin == math.MaxInt64 {
			tmpMin = -1
		}
		memo[amount-1] = tmpMin

		return tmpMin
	}

	return find(amount)
}

暴力+记忆优化题解请参考：https://leetcode-cn.com/problems/coin-change/solution/bao-li-jie-fa-jia-memo-you-hua-by-renydd-5n1r/

有以下几点需要在思考时提前想到：

动态规划是一个从下而上的方法；
选用归纳的方法思考，目标求 F(i) 时，则可假设你已有 F(0) 到 F(i-1) 到结果，而你所要寻找的就是如何推演

这道题的推演方式：F(i) 取自遍历所有 coins 时，对每一种硬币做了选择后进行比较，选取其与现有 F(i) 的最小值

func coinChange(coins []int, amount int) int {
	dp := make([]int, amount+1) // amount 值直接作为索引
	for i, _ := range dp {
		dp[i] = amount + 1 // 默认 todo
	}
	dp[0] = 0

	for i := 1; i <= amount; i++ {
		for j := 0; j < len(coins); j++ {
			if coins[j] <= i { // 不能用 i > coins[j]，否则会略过类似 i=1, coins[j]=1 时对 dp 的更新
				dp[i] = min(dp[i], dp[i-coins[j]]+1)
			}
		}
	}

	if dp[amount] > amount {
		return -1
	}
	return dp[amount]
}

# README

解题思路