# README
Package tensor 




 #
#
Package tensor is a package that provides efficient, generic (by some definitions of generic) n-dimensional arrays in Go. Also in this package are functions and methods that are used commonly in arithmetic, comparison and linear algebra operations.
The main purpose of this package is to support the operations required by Gorgonia.
Introduction
In the data analysis world, Numpy and Matlab currently reign supreme. Both tools rely heavily on having performant n-dimensional arrays, or tensors. There is an obvious need for multidimensional arrays in Go.
While slices are cool, a large majority of scientific and numeric computing work relies heavily on matrices (two-dimensional arrays), three dimensional arrays and so on. In Go, the typical way of getting multidimensional arrays is to use something like [][]T. Applications that are more math heavy may opt to use the very excellent Gonum matrix package. What then if we want to go beyond having a float64 matrix? What if we wanted a 3-dimensional float32 array?
It comes to reason then there should be a data structure that handles these things. The tensor package fits in that niche.
Basic Idea: Tensor
A tensor is a multidimensional array. It's like a slice, but works in multiple dimensions.
With slices, there are usage patterns that are repeated enough that warrant abstraction - append, len, cap, range are abstrations used to manipulate and query slices. Additionally slicing operations (a[:1] for example) are also abstractions provided by the language. Andrew Gerrand wrote a very good write up on Go's slice usage and internals.
Tensors come with their own set of usage patterns and abstractions. Most of these have analogues in slices, enumerated below (do note that certain slice operation will have more than one tensor analogue - this is due to the number of options available):
| Slice Operation | Tensor Operation |
|---|---|
len(a) | T.Shape() |
cap(a) | T.DataSize() |
a[:] | T.Slice(...) |
a[0] | T.At(x,y) |
append(a, ...) | T.Stack(...), T.Concat(...) |
copy(dest, src) | T.CopyTo(dest), tensor.Copy(dest, src) |
for _, v := range a | for i, err := iterator.Next(); err == nil; i, err = iterator.Next() |
Some operations for a tensor does not have direct analogues to slice operations. However, they stem from the same idea, and can be considered a superset of all operations common to slices. They're enumerated below:
| Tensor Operation | Basic idea in slices |
|---|---|
T.Strides() | The stride of a slice will always be one element |
T.Dims() | The dimensions of a slice will always be one |
T.Size() | The size of a slice will always be its length |
T.Dtype() | The type of a slice is always known at compile time |
T.Reshape() | Given the shape of a slice is static, you can't really reshape a slice |
T.T(...) / T.Transpose() / T.UT() | No equivalent with slices |
The Types of Tensors
As of the current revision of this package, only dense tensors are supported. Support for sparse matrix (in form of a sparse column matrix and dictionary of keys matrix) will be coming shortly.
Dense Tensors
The *Dense tensor is the primary tensor and is represented by a singular flat array, regardless of dimensions. See the Design of *Dense section for more information. It can hold any data type.
Compressed Sparse Column Matrix
Documentation Coming soon
Compressed Sparse Row Matrix
Documentation Coming soon
Usage
To install: go get -u "gorgonia.org/tensor"
To create a matrix with package tensor is easy:
// Creating a (2,2) matrix of int:
a := New(WithShape(2, 2), WithBacking([]int{1, 2, 3, 4}))
fmt.Printf("a:\n%v\n", a)
// Output:
// a:
// ⎡1 2⎤
// ⎣3 4⎦
//
To create a 3-Tensor is just as easy - just put the correct shape and you're good to go:
// Creating a (2,3,4) 3-Tensor of float32
b := New(WithBacking(Range(Float32, 0, 24)), WithShape(2, 3, 4))
fmt.Printf("b:\n%1.1f\n", b)
// Output:
// b:
// ⎡ 0.0 1.0 2.0 3.0⎤
// ⎢ 4.0 5.0 6.0 7.0⎥
// ⎣ 8.0 9.0 10.0 11.0⎦
//
// ⎡12.0 13.0 14.0 15.0⎤
// ⎢16.0 17.0 18.0 19.0⎥
// ⎣20.0 21.0 22.0 23.0⎦
Accessing and Setting data is fairly easy. Dimensions are 0-indexed, so if you come from an R background, suck it up like I did. Be warned, this is the inefficient way if you want to do a batch access/setting:
// Accessing data:
b := New(WithBacking(Range(Float32, 0, 24)), WithShape(2, 3, 4))
x, _ := b.At(0, 1, 2)
fmt.Printf("x: %v\n", x)
// Setting data
b.SetAt(float32(1000), 0, 1, 2)
fmt.Printf("b:\n%v", b)
// Output:
// x: 6
// b:
// ⎡ 0 1 2 3⎤
// ⎢ 4 5 1000 7⎥
// ⎣ 8 9 10 11⎦
// ⎡ 12 13 14 15⎤
// ⎢ 16 17 18 19⎥
// ⎣ 20 21 22 23⎦
Bear in mind to pass in data of the correct type. This example will cause a panic:
// Accessing data:
b := New(WithBacking(Range(Float32, 0, 24)), WithShape(2, 3, 4))
x, _ := b.At(0, 1, 2)
fmt.Printf("x: %v\n", x)
// Setting data
b.SetAt(1000, 0, 1, 2)
fmt.Printf("b:\n%v", b)
There is a whole laundry list of methods and functions available at the godoc page
Design of *Dense
The design of the *Dense tensor is quite simple in concept. However, let's start with something more familiar. This is a visual representation of a slice in Go (taken from rsc's excellent blog post on Go data structures):
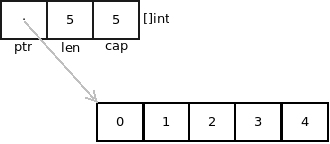
The data structure for *Dense is similar, but a lot more complex. Much of the complexity comes from the need to do accounting work on the data structure as well as preserving references to memory locations. This is how the *Dense is defined:
type Dense struct {
*AP
array
e Engine
// other fields elided for simplicity's sake
}
And here's a visual representation of the *Dense.
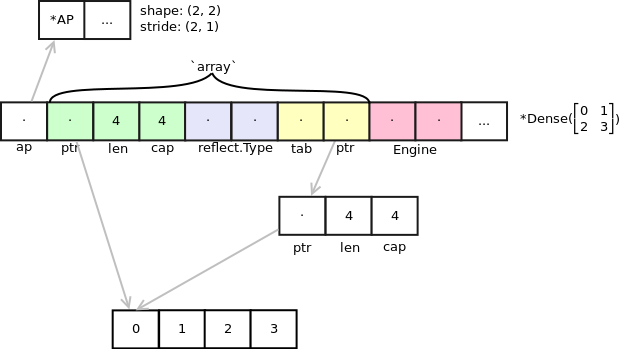
*Dense draws its inspiration from Go's slice. Underlying it all is a flat array, and access to elements are controlled by *AP. Where a Go is able to store its metadata in a 3-word stucture (obiviating the need to allocate memory), a *Dense unfortunately needs to allocate some memory. The majority of the data is stored in the *AP structure, which contains metadata such as shape, stride, and methods for accessing the array.
*Dense embeds an array (not to be confused with Go's array), which is an abstracted data structure that looks like this:
type array struct {
storage.Header
t Dtype
v interface{}
}
*storage.Header is the same structure as reflect.SliceHeader, except it stores a unsafe.Pointer instead of a uintptr. This is done so that eventually when more tests are done to determine how the garbage collector marks data, the v field may be removed.
The storage.Header field of the array (and hence *Dense) is there to provide a quick and easy way to translate back into a slice for operations that use familiar slice semantics, of which much of the operations are dependent upon.
By default, *Dense operations try to use the language builtin slice operations by casting the *storage.Header field into a slice. However, to accomodate a larger subset of types, the *Dense operations have a fallback to using pointer arithmetic to iterate through the slices for other types with non-primitive kinds (yes, you CAN do pointer arithmetic in Go. It's slow and unsafe). The result is slower operations for types with non-primitive kinds.
Memory Allocation
New() functions as expected - it returns a pointer of *Dense to a array of zeroed memory. The underlying array is allocated, depending on what ConsOpt is passed in. With New(), ConsOpts are used to determine the exact nature of the *Dense. It's a bit icky (I'd have preferred everything to have been known statically at compile time), but it works. Let's look at some examples:
x := New(Of(Float64), WithShape(2,2)) // works
y := New(WithShape(2,2)) // panics
z := New(WithBacking([]int{1,2,3,4})) // works
The following will happen:
- Line 1 works: This will allocate a
float64array of size 4. - Line 2 will cause a panic. This is because the function doesn't know what to allocate - it only knows to allocate an array of something for the size of 4.
- Line 3 will NOT fail, because the array has already been allocated (the
*Densereuses the same backing array as the slice passed in). Its shape will be set to(4).
Alternatively you may also pass in an Engine. If that's the case then the allocation will use the Alloc method of the Engine instead:
x := New(Of(Float64), WithEngine(myEngine), WithShape(2,2))
The above call will use myEngine to allocate memory instead. This is useful in cases where you may want to manually manage your memory.
Other failed designs
The alternative designs can be seen in the ALTERNATIVE DESIGNS document
Generic Features
Example:
x := New(WithBacking([]string{"hello", "world", "hello", "world"}), WithShape(2,2))
x = New(WithBacking([]int{1,2,3,4}), WithShape(2,2))
The above code will not cause a compile error, because the structure holding the underlying array (of strings and then of ints) is a *Dense.
One could argue that this sidesteps the compiler's type checking system, deferring it to runtime (which a number of people consider dangerous). However, tools are being developed to type check these things, and until Go does support typechecked generics, unfortunately this will be the way it has to be.
Currently, the tensor package supports limited type of genericity - limited to a tensor of any primitive type.
How This Package is Developed
Much of the code in this package is generated. The code to generate them is in the directory genlib2.
Things Knowingly Untested For
complex64andcomplex128are excluded from quick check generation process Issue #11
TODO
- Identity optimizations for op
- Zero value optimizations
- fix Random() - super dodgy
How To Get Support
The best way of support right now is to open a ticket on Github.
Contributing
Obviously since you are most probably reading this on Github, Github will form the major part of the workflow for contributing to this package.
See also: CONTRIBUTING.md
Contributors and Significant Contributors
All contributions are welcome. However, there is a new class of contributor, called Significant Contributors.
A Significant Contributor is one who has shown deep understanding of how the library works and/or its environs. Here are examples of what constitutes a Significant Contribution:
- Wrote significant amounts of documentation pertaining to why/the mechanics of particular functions/methods and how the different parts affect one another
- Wrote code, and tests around the more intricately connected parts of Gorgonia
- Wrote code and tests, and have at least 5 pull requests accepted
- Provided expert analysis on parts of the package (for example, you may be a floating point operations expert who optimized one function)
- Answered at least 10 support questions.
Significant Contributors list will be updated once a month (if anyone even uses Gorgonia that is).
Licence
Gorgonia and the tensor package are licenced under a variant of Apache 2.0. It's for all intents and purposes the same as the Apache 2.0 Licence, with the exception of not being able to commercially profit directly from the package unless you're a Significant Contributor (for example, providing commercial support for the package). It's perfectly fine to profit directly from a derivative of Gorgonia (for example, if you use Gorgonia as a library in your product)
Everyone is still allowed to use Gorgonia for commercial purposes (example: using it in a software for your business).
Various Other Copyright Notices
These are the packages and libraries which inspired and were adapted from in the process of writing Gorgonia (the Go packages that were used were already declared above):
| Source | How it's Used | Licence |
|---|---|---|
| Numpy | Inspired large portions. Directly adapted algorithms for a few methods (explicitly labelled in the docs) | MIT/BSD-like. Numpy Licence |