树结构

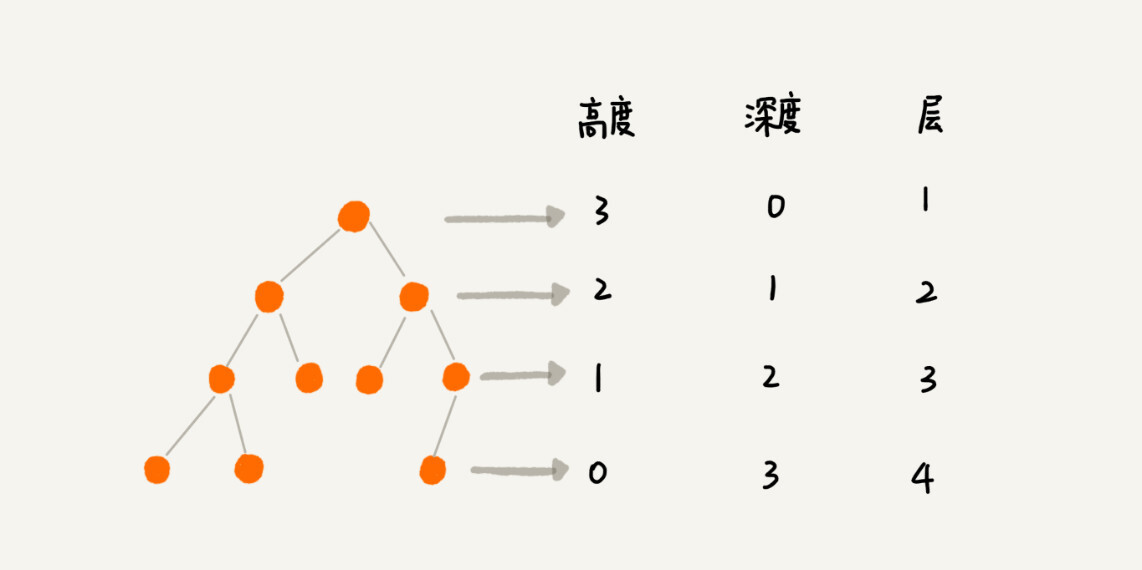
树的相关概念：高度，深度，层。

1. 完全二叉树： 叶子节点都在最底下两层，最后一层的叶子节点都靠左排列，并且除了最后一层，其他层的节点个数都要达到最大，这种二叉树叫作完全二叉树。
2. 满二叉树：特殊的完全二叉树

完全二叉树适合用数组进行存储，最节省空间。因为数组的存储方式并不需要像链式存储法那样，要存储额外的左右子节点的指针。非完全二叉树适合链式存储。为什么完全二叉树适合数组存储？

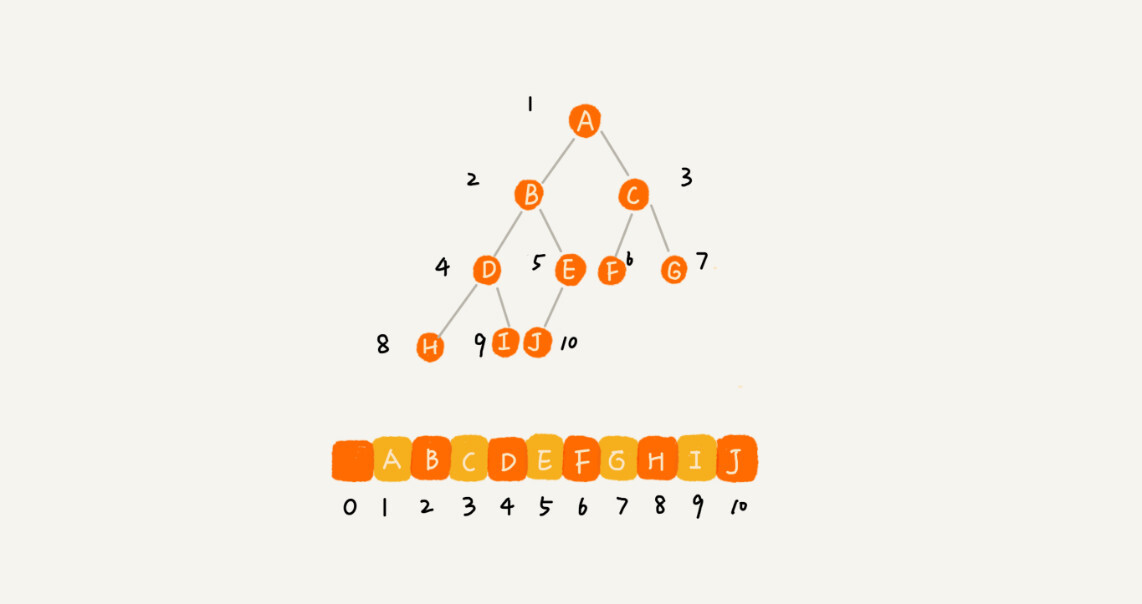
完全二叉树：由下图可以观察到，仅仅浪费了数组0位置空间。对于任意节点索引为i，其左子节点索引为2i，其右子节点索引为2i+1。

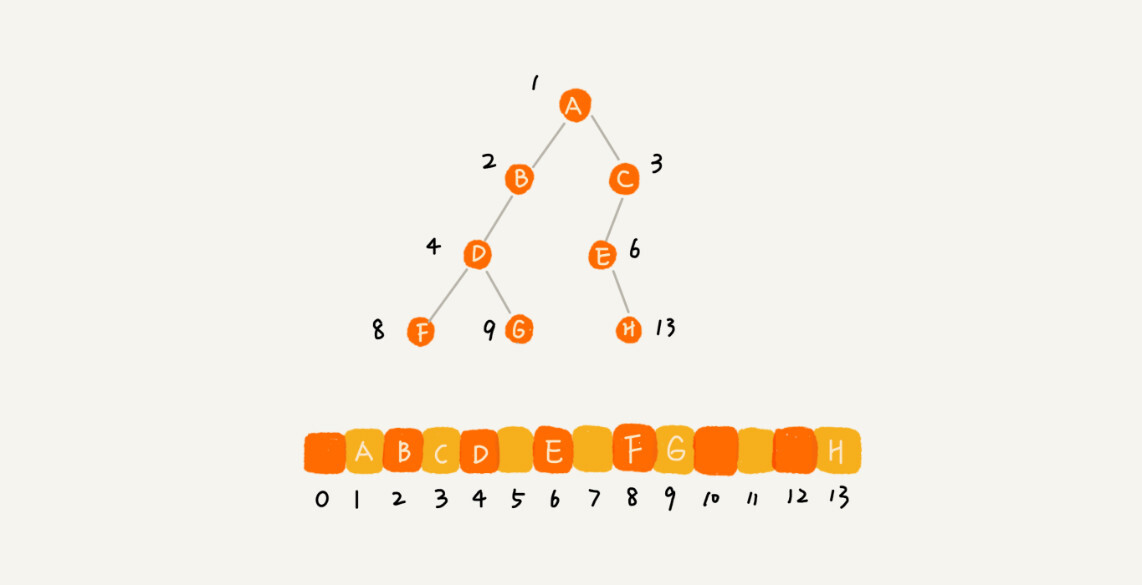
非完全二叉树：由下图可以观察到除了0位置外，很多节点的空间都被浪费掉了。

二叉树的遍历

树的遍历方式：

1. 前序遍历：对于树中的任意节点来说，先打印这个节点，然后再打印它的左子树，最后打印它的右子树。
2. 中序遍历：对于树中的任意节点来说，先打印它的左子树，然后再打印它本身，最后打印它的右子树。
3. 后序遍历：对于树种的任意节点来说，先打印它的左子树，然后打印它的右子树，最后打印这个节点本身。

二叉树相对于散列表的优势

1. 散列表是无序的，遍历需要重新排序
2. 散列表扩容耗时多
3. 散列表冲突时，性能不稳定
4. 散列表的构建比二叉树要复杂得多，需要考虑散列函数的设计

二叉树的增删改查

平衡二叉树

由于普通二叉树在极端情况下，会退化成链表，时间复杂度退化成O（logn），所以平衡二叉树应运而生。

AVL：高度平衡二叉树，查找效率高，但是增加和删除时为了维持高度平衡，每次都需要调整平衡树。对于频繁插入和删除的集合，使用AVL树不太合适。

红黑树：只做到了近似平衡，插入、删除、查找都比较稳定。